2 Transverse stability
The aim of this chapter is to answer the question; is transverse stability an important factor in Moth design, and is the WSH design sufficiently stable ?
2.1 Comparison of GZ curve data
The Wolston Unit’s hydrostatics program was used to evaluate the two designs by providing stability data for the hull forms heeled up to seventy degrees. Seventy degrees is assumed to be the point of capsize. To isolate the hydrostatic GZ data the centre of gravity of the two designs was put on the waterline.
Axeman Data
Displacement = 0.1 Tonnes
Longitudinal centre of gravity = -0.018 Metres
Vertical centre of gravity = 0.0 Metres
GM = 0.056 Metres
Ship length = 3.355 Metres
Roll centre = 0.0
Specific gravity of water = 1.0250
Table 2.1
GZ data for the Axeman hull form.
| Heel angle degrees | Righting lever (GZ) m | Waterline m | Trim m | GZ curve area m.Rad | Righting lever N.M |
| 0 | 0.000 | 0.008 | -0.001 | 0.000 | 0.0 |
| 10 | 0.010 | 0.007 | -0.002 | 0.001 | 9.81 |
| 20 | 0.022 | 0.005 | -0.005 | 0.004 | 21.58 |
| 30 | 0.035 | 0.001 | -0.015 | 0.009 | 34.34 |
| 40 | 0.049 | -0.008 | -0.031 | 0.016 | 48.07 |
| 50 | 0.073 | -0.023 | -0.054 | 0.026 | 71.61 |
| 60 | 0.102 | -0.044 | -0.080 | 0.042 | 100.06 |
| 70 | 0.121 | -0.064 | -0.101 | 0.061 | 118.70 |
WSH Data
Displacement = 0.1 Tonnes
Longitudinal centre of gravity = -0.047 Metres
Vertical centre of gravity = 0.0 Metres
GM = 0.038 Metres
Ship length = 3.355 Metres
Roll centre = 0.0
Specific gravity of water = 1.0250
Table 2.2
GZ data for the WSH hull form.
| Heel angle degrees | Righting lever (GZ) m | Waterline m | Trim m | GZ curve area m.Rad | Righting lever N.M |
| 0 | 0.000 | -0.001 | -0.000 | -0.000 | 0.0 |
| 10 | -0.006 | -0.001 | -0.000 | -0.001 | -5.89 |
| 20 | -0.012 | -0.003 | -0.001 | -0.002 | -11.77 |
| 30 | -0.014 | -0.004 | -0.004 | -0.004 | -13.73 |
| 40 | -0.012 | -0.008 | -0.007 | -0.007 | -11.77 |
| 50 | 0.011 | -0.016 | -0.021 | -0.007 | 10.79 |
| 60 | 0.045 | -0.028 | -0.035 | -0.002 | 44.15 |
| 70 | 0.074 | -0.040 | -0.044 | 0.008 | 72.59 |
Clearly from the graph of the GZ curves for the two hull forms ( fig 2.1 ) the WSH design is much more unstable than the Axeman. To understand the craft's stability fully we must analyse all the components that contribute to its stability
2.2 Stability components

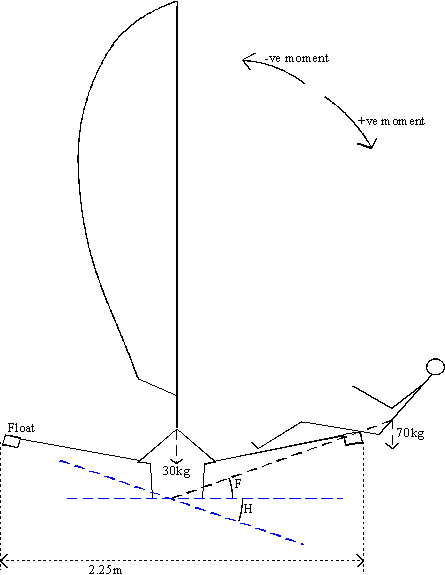
The sailor has a mass of seventy kilograms at a lever to the centreline of approximately 1.425 metres, if the heel angle (H) is zero. This gives a moment of
70×9.81×1.425 = 979 Nm
This shall be the magnitude of one unit moment. In this case it is acting in a positive clockwise direction. The sailor is at an offset angle F so the moment will vary according to the relationship
cos(W+F)
A realistic value of F is thirty degrees so the sailor’s mass unit moment is equal to
cos(H+30)/cos(30)
The vertical centre of gravity of the rigged craft is assumed to be 75 cm above the waterline so it’s component will be equal to
30×9.81×0.75×sin(H)
The GZ righting moment will corrected by adding the realistic centre of gravity and dividing by 979 Nm to make it into a unit form.
There is a float on the ends of both wings; these will provide 0.4 units of moment when submerged. A realistic assumed value of the heel angle at which they submerge is 25 degrees.
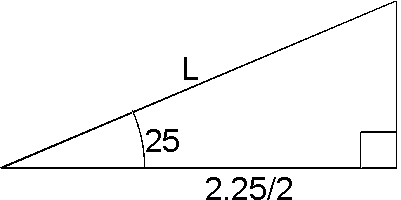
2.25/2L = cos(25)
L = 1.24 m
0.4×979 = 1.24×B
B = 316 N = 32 kg
The dimensions of the floats are approximately 2 m by 0.16 m by 0.1 m. This gives a buoyancy of
2×0.1×0.16×1025 = 32.8 kg
Note that the immersion of the floats will reduce the displacement of the hull to 67 kilograms, this will decrease the magnitude of the hulls GZ curve. This effect has not been incorporated into the analysis because, as shall be seen, it is small compared to the magnitude of the other components of stability.
According to B. Deakin’s paper "The development of stability standards for UK sailing vessels" : "Navel Architects concerned with yacht performance assume that the heeling moment varies with cos(H). This assumption was validated in the wind tunnel tests for close hauled sailing conditions up to heel angles of about thirty degrees." So in unit form the moment for the sail and dagger board interaction for angles up to thirty degrees is equal to
-cos(H)
For angles greater than thirty degrees we shall also assume this relationship to be valid. Although this is not an accurate relationship in this region it will allow us to continue this crude analysis without extensive wind tunnel tests.
The moment from the sail acts in a negative anticlockwise direction and is equal to negative one when H is equal to zero. The total moment on the craft is zero when the craft is sailing close hauled and upright. This is to simulate the a quasi-static equilibrium sailing state. The total moment on the craft as it deviates slightly from this angle and the effect of the floats when angles are greater, can be investigated.
Table 2.3
Calculated quasi-static stability for the WSH design.
| H | Unit sail moment | Sailor’s unit mass moment | Unit GZ moment | Unit wing buoyancy moment | Sailor + GZ + wing | Total moment |
| -30 | -0.866 | 1.155 | 0.127 | -0.400 | 0.972 | 0.106 |
| -20 | -0.940 | 1.137 | 0.089 | 0.000 | 1.226 | 0.286 |
| -10 | -0.985 | 1.085 | 0.045 | 0.000 | 1.130 | 0.145 |
| 0 | -1.000 | 1.000 | 0.000 | 0.000 | 1.000 | 0.000 |
| 10 | -0.985 | 0.885 | -0.045 | 0.000 | 0.840 | -0.145 |
| 20 | -0.940 | 0.742 | -0.089 | 0.000 | 0.635 | -0.305 |
| 30 | -0.866 | 0.577 | -0.127 | 0.400 | 0.850 | -0.016 |
| 40 | -0.766 | 0.395 | -0.157 | 0.394 | 0.632 | -0.134 |
| 50 | -0.643 | 0.201 | -0.162 | 0.376 | 0.415 | -0.228 |
| 60 | -0.500 | 0.000 | -0.150 | 0.346 | 0.196 | -0.304 |
| 70 | -0.342 | -0.201 | -0.138 | 0.306 | -0.033 | -0.375 |
Figure 2.2 plots the above data in table 2.3 and reveals that there are no areas of stability. The total moment curve has a negative gradient for small angles away from upright, which indicates that any deviation away from upright will be amplified.
Would the Axeman be any more stable than the WSH design ? I shall examine both boats’ total moment curve with the same conditions but different GZ curves.
Table 2.4
Calculated quasi-static stability for both designs.
| H | Sail moment | GZ Axeman | GZ WSH | Sailor + wing | Total Axeman | Total WSH |
| -30 | -0.866 | 0.078 | 0.127 | 0.755 | 0.037 | 0.106 |
| -20 | -0.940 | 0.055 | 0.089 | 1.137 | 0.296 | 0.286 |
| -10 | -0.985 | 0.029 | 0.045 | 1.085 | 0.149 | 0.145 |
| 0 | -1.000 | 0.000 | 0.000 | 1.000 | 0.000 | 0.000 |
| 10 | -0.985 | -0.029 | -0.045 | 0.885 | -0.129 | -0.145 |
| 20 | -0.940 | -0.055 | -0.089 | 0.742 | -0.259 | -0.305 |
| 30 | -0.866 | -0.078 | -0.127 | 0.977 | 0.033 | -0.016 |
| 40 | -0.766 | -0.096 | -0.157 | 0.789 | -0.073 | -0.134 |
| 50 | -0.643 | -0.100 | -0.162 | 0.577 | -0.166 | -0.228 |
| 60 | -0.500 | -0.093 | -0.150 | 0.346 | -0.247 | -0.304 |
| 70 | -0.342 | -0.091 | -0.138 | 0.105 | -0.328 | -0.375 |
Figure 2.3 illustrates that the is no significant change in the total moment curve. So although the Axeman is more stable the overall difference is small.
2.3 Investigation into the craft stability with a heeled mast
The quasi-static conditions shall be kept the same, except that the mast will be heeled to leeward (negative sense) by twenty degrees. The effect this will have on the overall stability can be investigated. The unit sail moment is now equal to
cos(H+20)/cos(20)
Table 2.5
Calculated quasi-static stability data for the WSH design with the mast heeled to leeward.
| H | Unit sail moment | Sailor+GZ+wings | Total moment |
| -30 | -1.048 | 0.972 | -0.076 |
| -20 | -1.064 | 1.226 | 0.162 |
| -10 | -1.048 | 1.130 | 0.082 |
| 0 | -1.000 | 1.000 | 0.000 |
| 10 | -0.922 | 0.840 | -0.082 |
| 20 | -0.815 | 0.635 | -0.180 |
| 30 | -0.684 | 0.850 | 0.166 |
| 40 | -0.532 | 0.632 | 0.100 |
| 50 | -0.364 | 0.415 | 0.051 |
| 60 | -0.185 | 0.196 | 0.011 |
| 70 | 0.000 | -0.033 | -0.033 |
Figure 2.4 illustrates that heeling the mast to leeward dramatically increased the stability of the craft. Not only are there areas of stability but the gradient of the curve around the upright area is shallower. This indicates that the craft is about two times more stable than the craft with an upright mast.
2.4 Transverse stability conclusions
How does a boat that spends most or all of it’s time in a state of instability sail upright?
Moths are very demanding boats to sail. The main sheet and rudder must be adjusted constantly to keep the craft sailing at the right angle of heel. The sail and foils add a large component of damping into the system making the task of sailing possible.
An acceptable value of transverse stability must be defined. This value will vary between sailors and sailing conditions. It shall be concluded that in general the vertical centre of gravity height, wing bar angle, float size and heel angle of the mast are far more significant to transverse stability than GZ curves. The Axeman has sufficient stability in the opinion of the author and most Moth sailors; so due to the overriding dynamics of the situation I shall conclude that the stability of the WSH design will also be acceptable.
Although this analysis has helped us to understand the dynamics of the situation it may be fair to say that it is fundamentally flawed. It has not attacked the real causes of capsizes, which occur during tacks, gibes or light winds. These happen because the sailor does not always have the damping effect of the sail working at its full potential. The additional stability of the floats and the large damping experienced when the wing is dragged through the water along with the sailor's skill are key components in these situations.
A Moth heeled to windward by 20° ( H= -20) will enable 19 % more righting moment to be achieved. This explains why in strong winds the boats are often sailed heeled to windward. The loss of efficiency of the rig and dagger board is played off against the greater righting moment. More righting moment means the rig can be sheeted in harder and a potential increase in driving force obtained.
In the limited wind speed range between being over and under powered there is a potential advantage in raking the mast to leeward by twenty degrees and heeling the boat to windward by twenty degrees. This advantage must be considered against the extra complication whist tacking and the additional weight of the extra rig control system. Tacking is hard enough without having to wave the mast through forty degrees. So as the range of conditions where this would be an advantage is small and, due to the practicality of operating the system effectively, I shall conclude that the idea is not worth employing at this stage. However a Swiss Moth sailor has had a similar system on his boat for a year.