7 Mast Design
7.1 Loads on the Mast
It is very hard to determine accurate working and maximum loads on the equipment of a Moth without strain gauging the boat during sailing trials. However a crude analysis of these loads to try to determine the working loads on a Moth mast is shown below. These calculated loads are quasi-static; they increase understanding of the loads on the rig but the analysis is only as good as the assumptions made during it.
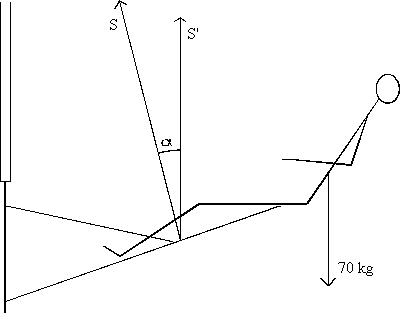
Shroud tension when sailing close hauled or reaching

S' = the vertical component of tension in the shroud which is approximately twice the sailor's weight = 1400 Newtons
a
= the angle of the shroud to the vertical axiss = the shroud tension
s » 1400 / cos 15 = 1450 N
Assuming the leeward shroud to be slack.
I shall assume that a sailor can pull 300 N of force on the main sheet. This goes through a 4:1 purchase onto the boom, so the total force is 1200 N. The kicker tension is assumed to be slack when the main sheet is pulled with 300 N of force.
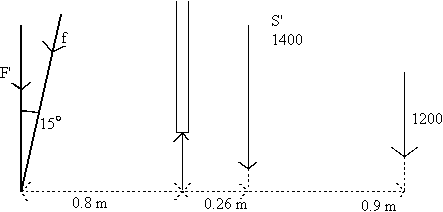
Taking moments fore and aft about the mast step.
F' x 0.8 = 1400 x 0.26 + 0.9 x 1200
F' = 1805 N
f = 1805 / cos 15 = 1869 » 1870 N
So upwind some of the normal working loads are as follows:-
Forestay tension = f » 1900 N
Shroud tension = s » 1500 N
The compression load on the mast (C) between the hounds and mast step, when sailing upwind can be found by resolving forces vertically.
A luff tension load on the mast has been included. This load is assumed to be equal to a 300 N pull on a 6 : 1 cunningham control line. Compression loads due to halyards running inside the mast have not been included because the moth does not have a halyard.
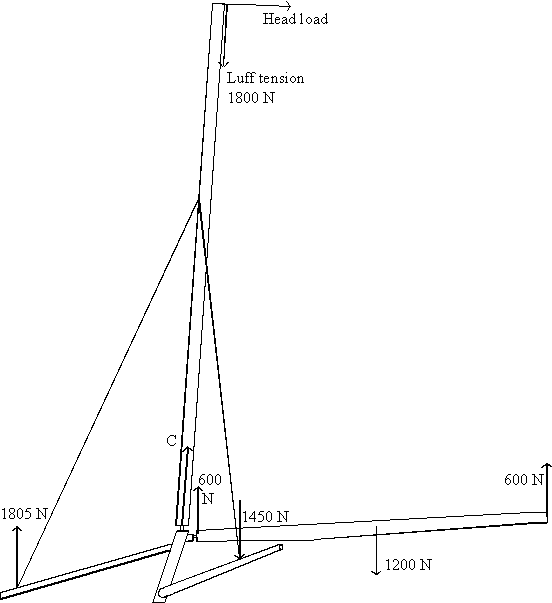
C = 1805 + 1450 + 600 + 1800 = 5655 N
Head load = Bending moment on boom from main sheet / mast length
0.9 x 1200 / 5.25 = 206 N
Shroud Tension when sailing down wind
From the calculation of longitudinal stability the nose diving moment with the bow down by 20 cm at 6 knots is 1405 Nm. Assuming that at the forestay is slack and the two shrouds share the load equally the compression load, C can be found as follows.
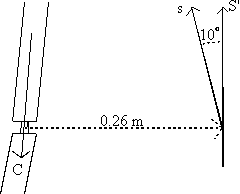
The nose diving moment is produced by the shrouds and compression loads on the mast.
C = S'
1405 = C x 0.26
C = 5404N
The combined shroud tension s = S' / cos 10 = 5404 / cos 19 = 5487 N
The total compression load including the luff tension of 1800 N and main sheet down force 600 N is
C = 5404 + 1800 + 600 = 7804 N
7.2 Mast Specification
From the above analysis of the normal working loads on the mast the following specification for the mast can be defined.
The mast must withstand the maximum compressive working load to allow for gusts, nose dives and severe conditions. A safety factor (Sf) must be introduced.
\ max compressive load = Sf ´ 7804
A suitable value of Sf should be chosen however it is seen later that Sf is less than 1.
The section shall be circular so that the camber inducers work well and it will also be an easy section to fabricate.
The mast shall consist of to parts, a uniform section between the hounds and the mast foot and a tapered top section above the hounds.
The diameter of the section shall be a compromise between the following factors;
·
a small diameter mast will reduce windage.
· a large diameter mast will be lighter than a smaller diameter mast with the same stiffness
· a large diameter mast will have thin walls and is therefore be very fragile and may fail due to impact damage.
The stiffness of the mast has a large effect on the performance of the rig. It is therefore important to get the right bend characteristics from the mast. Achieving the right bend characteristics with uni-directional fibres is easier than defining what the optimum bend characteristics are.
The easiest way to determine competitive mast bend characteristics is to mimic an existing competitive mast. The stiffness of an existing mast can be determined from tests and measurements. A composite lay-up that will achieve the same characteristics can then be designed. If the mast designer feels that the characteristics of the mast and rig could be improved upon then modifications to the lay-up can be included at this stage.
7.3 Mast Design Example
A carbon fibre mast for a camber induced sail is used to provide a competitive parent mast to mimic. The mast is analysed in two parts
i) the main section between the hounds and step
ii) the tapered top.
i) Main mast section design
The parent mast was tested by adding weights to it and measuring the deflections. The mast is modelled as a uniform beam.
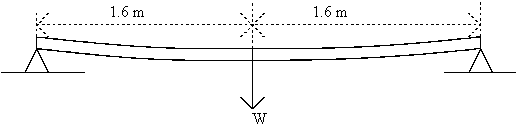
From beam theory
y = W.L3 / 48.E.I
where
W = applied load = 302 Newtons
L = section length = 3.2m
E = Young's modulous for mast material
I = second moment of area of section
y = deflection in the middle of the mast
y = 0.028 = (302 ´ 3.23) / 48 EI
EI = 7363
This test was done to measure the section modulous fore and aft as well as side to side. The mast was found to have the same characteristics in both cases.
Note that the buckling load (W) for the masts section can be found using the Euler critical load calculation.
W = p 2 EI / L2
For a beam that is simply supported at each end.
W = p 2 7363 / 3.22 = 7097 N
This load is less than the calculated working load but the mast has not broken in service. Either the analysis of the loads on the rig is inaccurate or the effective length of the mast is less than the geometrical length. The spreaders, which were not included in the analysis of the working loads or buckling load, must offer the mast a lot of support. Clearly the analysis of the rig loads is not accurate enough for design purposes.
The lay-up of the mast will consist of 2 layers of uni-directional fibres wound around its circumference sandwiching a layer of unidirectional fibres running up and down the length of the mast. The longitudinal fibres are to give the mast the desired properties and the two circumferential layers will provide the mast with hoop-wise strength so that it will not burst apart and will have more impact strength.
The composite lay-up is illustrated in this diagram
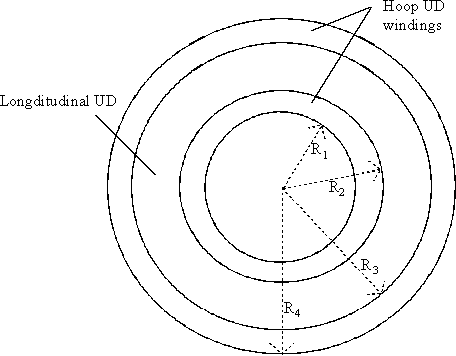
EI for the section can be calculated as follows.
I = p /4 (RE4 - RI4) for a tube
\
EI = p /4 ET[(R24 - R14) + (R44 - R34)] + p /4 EL[(R34 - R24)where
ET = modulous of hoop winding composite
EL = modulous of UD longitudinal composite
If the mast has different properties when bent about different axis the section lay-up can be calculated as follows.
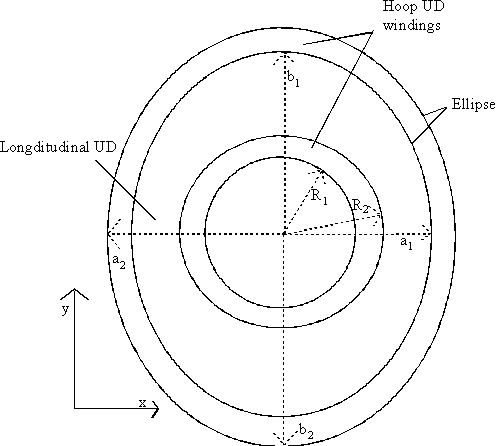
I = p /4 (ab3) for ellipse
I = p /4 (RE4 - RI4) for tube
EIX = ET [p /4 (R24 - R14) + p /4 (a2b23 - a1b13)] + ELp /4 (a1b13 - R24)
EIY = ET [p /4 (R24 - R14) + p /4 (a23b2 - a13b1)] + ELp /4 (a13b1 - R24)
To determine appropriate values of R1, R2, R3 and R4 values of ET and EL have to be calculated. The modulous of the composite will depend on the fibres used, the volume fraction achieved, the fibre orientation and the quality of the laminate. Accurate values can only really be determined by stressing test pieces. However the following values for the composite properties are assumed to be sufficiently accurate. Data is taken from "Analysis and Performance of Fibre Composites" by Agarwal and Broutman.
Composites are to be fabricated from Thornel 300 graphite fibres and epoxy resin.
Resin properties
( at 23° C )
s Y = 90 MPa
E = 3.4 GPa
r = 1250 kg/m3
UD composite longitudinal properties
( at 0° C )
tensile s Y = 1725 MPa
compressive s Y = 1366 MPa
tensile E = 159 GPa
compressive E = 138 GPa
average EL = 149 GPa
Volume fraction = 63
r = 1610 kg/m3
UD composite transverse properties
( at 0° C )
r = 1610 kg/m3
Volume fraction = 63
The transverse properties of this UD composite can be calculated using the Halpin-Tsai equations
ET/Em = (1 + x h Vf) / (1 - h Vf)
h
= [(Ef/Em) - 1] / [(Ef/Em) + x ]where
x
= 2 for cylindrical fibresEC = Ef ´ Vff + Em ´ Vfm
where
EC = composite modulous
Ef = fibre modulous
Vff = volume fraction of fibres
Vfm = volume fraction of the matrix
148 = Ef x 0.63 + 3.4 x 0.37
Ef = 233 GPa
Therefore the transverse modulous of the composite is calculated as follows;
h = [(233/3.4) -1] / [(233/3.4) + 2] = 0.957
ET/Em = (1 + 2 x 0.975 x 0.63) / (1 - 0.957 x 0.63) = ET/3.4
ET/Em = 5.55
ET = 18.9 GPa
For this particular worked example;
4 EI / p = ET [(R24 - R14) + (R44 - R34)] + EL(R34 - R24)
However ET << EL so the tube shall be modelled with all its unidirectional fibres running longitudinally. This makes the analysis a lot simpler but it is not exact and will only work if thin walled tubes are considered.
RI = internal radius
RE = external radius
t = thickness of the hoop windings layers
RI = R2 - ( ET / EL )´ t
RE = R3 + ( ET / EL )´ t
4 EI / p = EL ( RE4 -RI4 )
RE4 -RI4 = 4 ´ 7363 / ( p ´ 149´ 109 )
A suitable value of t is assumed to be 0.5 mm. An approximation of the tube weight per metre length can be included into the analysis to help select the optimum mast diameter.
Weight of the hoop windings = 2 ´ p ´ R ´ 2 ´ t ´ r
Approximate weight of tube = ( T + 2 t ) ´ 2 R r p
where
T = thickness of the tube
r = 1610 kg / m
R = RI
Table 7.1
Mast section radii and weight.
| RI m |
RE m |
T mm |
Tube weight kg |
| 0.0150 | 0.0184 | 3.36 | 0.662 |
| 0.0175 | 0.0199 | 2.40 | 0.602 |
| 0.0200 | 0.0217 | 1.73 | 0.552 |
| 0.0225 | 0.0238 | 1.27 | 0.517 |
| 0.0250 | 0.0260 | 0.95 | 0.493 |
| 0.0275 | 0.0282 | 0.73 | 0.481 |
| 0.0300 | 0.0306 | 0.57 | 0.476 |
Figure 7.1 shows how the tubes weight varies with diameter. From this graph and the fact that the tube thickness T should be greater than 2 mm for adequate damage resistance the internal radius of the mast shall be chosen to be 2.25 cm. This is the external radius of the mandrill used to fabricate the mast. The exact properties of the mast are as follows.
R1 = 0.0225 m
R2 = R1 + t = 0.023 m
RI = R2 - ( ET / EL )´ t
RI = 0.023 - (18.9/149)´ 0.0005 = 0.02294
RE4 -RI4 = 4 ´ 7363 / ( p ´ 149´ 109 )
RE = 0.02414
RE = R3 + ( ET / EL )´ t
R3 = 0.02414 - (18.9/149)´ 0.0005 = 0.02408 m
R4 = R3 + t = 0.02458 m
EI = p /4 ET [(R24 - R14) + (R44 - R34)] + p /4 EL(R34 - R24)
EI =p /4 18.9´ 109 [(0.0234 - 0.02254) + (0.024584 - 0.024084)]
+ p /4 149´ 109(0.024084 - 0.0234)
EI =7375
The section is 1.6% stiffer than parent mast. This inaccuracy is due to the thin wall tube assumption.
Bottom section tube weight = L.r .p (R42 - R12) = 1.585 kg
The tube wall thickness is 2.08 mm
ii) Tapered top section design
Beam theory can not be applied to tapered beams so bend tests will not yield section data. Another technique for analysing the parent mast must be developed. The second moment of area of the section can be calculated by measuring the dimensions of the section. The Young's modulous of the material is not as easy to measure if the mast is made from composite materials because it is hard to ascertain in which direction the fibres are oriented.
The section modulous of the taper the just above hounds will be the same as the section modulous bellow the hounds, so that there is no discontinuity in the tube's bend characteristics with a sudden change in section. The radius of the parent mast decreases linearly. The wall thickness is observed to be constant all the way along the mast. This is probably because this carbon mast was modelled on an aluminium mast which had a constant wall thickness.
To make a reasonable approximation of the parent mast the section modulous of the very tip needs to be calculated. The taper will simply be a constant wall thickness straight taper form the tip section to the main mast section modulous found earlier.
Parent mast data
wall thickness = 1.75 mm
Main section internal radius = 0.02575 m
Main section external radius = 0.0275 m
Tip section internal radius = 0.0095 m
Tip section external radius = 0.01125 mm
EC I = E p /4 (RE4 - RI4)
7363 = EC p /4 (0.02754 - 0.025754)
EC = 70.9´ 109
EC = the Young's modulous for the laminated composite.
EC shall be assumed to be constant. This assumption and will only be true if the laminate is constant in its proportions.
At the tip the section modules will be;
ECI = 70.9´ 109 p /4 (0.011254 - 0.00954)
ECI = 438.4
The section of the new mast design at the tip will be the same but the laminate will be different. The wall thickness must remain at 2.08 mm.
ECI = 7375 = EC p /4 (0.024584 - 0.02254)
EC = 86.4´ 109
EI = 86.4´ 109 p /4 (RE4 - RI4) = 438.4
RE4 - RI4 = 6.4605´ 10-9
This problem can be solved by an iterative process. The dimensions of the tip section are found to be;
Internal radius = 8.11 mm
External radius = 10.19 mm
Wall thickness = 2.08 mm
EI for tip = 436.1